Earn this, Earn it.
알고리즘 - 이진 검색과 비트조작 본문
이진 검색(Binary Search)이란?
정렬된 배열에서 타겟을 찾는 검색 알고리즘이다.
이진 검색은 값을 찾아내는 시간 복잡도가 O(log n)이라는 점에서 대표적인 로그 시간 알고리즘이며, 이진 탐색 트리 (Binary Search Tree)와도 유사한 점이 많다. 그러나 이진 탐색 트리가 정렬된 구조를 저장하고 탐색하는 '자료구조'라면, 이진 검색은 정렬된 배열에서 값을 찾아내는 '알고리즘' 자체를 지칭한다.
이진 탐색 트리는 1억 개의 아이템도 단 27번이면 모두 찾아낼 수 있다...

또 다른 유의점은 2^n은 금방 커질 수 있다는 것이다. 27번째 수부터 1억이 넘어가기 시작하고 기하급수적으로 커진다. O(2^n)은 얼핏 보면 O(n^2)과 비슷해 보이지만 실제로는 훨씬 더 크므로 시간 복잡도를 계산할 때 주의해야 한다.
Q. 정렬된 nums를 입력받아 이진 검색으로 target에 해당하는 인덱스를 찾아라.
입력
nums = [ -1, 0, 3, 5, 9, 12], target = 9출력
4
방법 1. 재귀
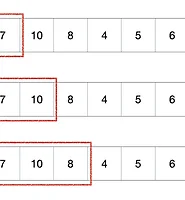
- 먼저 재귀로 이진 검색을 구현할 수 있다. 절반씩 범위를 줄여가며 맞출 때까지 재귀 호출을 하는 것이다.
class Solution:
def search(self, nums: List[int], target: int) -> int:
def binary_search(left, right):
if left <= right:
mid = (left + right) // 2
if nums[mid] < target:
return binary_search(mid + 1, right)
elif nums[mid] > target:
return binary_search(left, mid - 1)
else:
return mid
else:
return -1
return binary_search(0, len(nums) - 1)
방법 2. 반복
- 반복 풀이로도 풀 수 있다. 대개는 재귀 풀이가 더 우아한 편이지만, 반복 풀이는 좀 더 직관적이라 이해하기 쉽다.
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
else:
return mid
return -1
방법 3. 이진 검색 모듈
- 사실 파이썬에서는 이진 검색을 직접 구현할 필요가 없다. 이를 지원하는 bisect 모듈을 기본으로 제공하기 때문이다. 이 모듈을 이용하면 이진 검색을 파이썬다운 방식으로 간단히 풀이할 수 있다.
- 단 조심할 것은, 리스트 내에 원하는 요소가 없으면 리스트 크기보다 큰 인덱스를 반환한다는 점이다.
import bisect
class Solution:
def search(self, nums: List[int], target: int) -> int:
index = bisect.bisect_left(nums, target)
if index < len(nums) and nums[index] == target:
return index
else:
return -1
방법 4. 이진 검색을 사용하지 않는 index 풀이
- 파이썬에서 제공하는 index() 메서드를 활용하는 방법이다. 이 경우 존재하지 않는 값이라면 에러가 발생하므로 ValueError를 예외 처리하여 -1을 리턴하도록 처리하는 방법이 가능하다!
단, 이 방법은 이진 검색이 아니며, 이진 검색을 요구하는데 이렇게 풀이해선 안된다. 경우에 따라 패널티를 받을 수도 있다.
class Solution:
def search(self, nums: List[int], target: int) -> int:
try:
return nums.index(target)
except ValueError:
return -1
모든 풀이는 속도 차이가 거의 없으나 재귀를 이용한 풀이가 가장 느린 편이다. 실제로 코딩 테스트 시에는 가급적 재귀나 반복으로 직접 이진 검색을 풀이하는 편이 나중에 코드 리뷰를 하게 되는 경우 더 좋은 평가를 받을 수 있을 것이다.
이진 검색 알고리즘 버그
mid = (left + right) // 2
이렇게 두 값의 중간값을 구하게 되면 수학적으로 문제는 없으나 컴퓨터 과학에서는 문제를 일으킬 수 있다. 두 수를 더하면 항상 각각의 수보다 큰 수가 되며, 자료형에는 최댓값이 있다. 만약 left+right가 자료형의 최댓값을 넘어선다면, 예상치 못하는 결과나 오류가 발생한다. 즉 오버플로(Overflow)가 발생하는 것이다. 이를 방지하려면
mid = left + (right - left) //2와 같은 방식이 좋을 것이다.
Q. 두 배열의 교집합을 구하라.
<예제 1>
입력
nums1 = [1,2,2,1], nums2 = [2,2]출력
[2]<예제2>
입력
nums1 = [4,9,5], nums2 = [9,4,9,8,4]출력
[9,4]
어떤 풀이가 떠오르는가?
방법1. 이진 검색
- 한쪽은 순서대로 탐색하고 다른 쪽은 정렬해서 이진 검색으로 값을 찾으면, 검색 효율을 획기적으로 높일 수 있다. 이 경우 시간 복잡도는 O(n log(n))일 것이다. (정렬n log(n), nums1 반복 O(n), nums2 이진 검색 O(log n))
import bisect
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
result: Set = set()
nums2.sort()
for n1 in nums1:
# 이진 검색으로 일치 여부 판별
i2 = bisect.bisect_left(nums2, n1)
if len(nums2) > 0 and len(nums2) > i2 and n1 == nums2[i2]:
result.add(n1)
return result
방법2. 투 포인터
- 이 문제는 양쪽 다 정렬하여 투 포인터로 풀이할 수도 있다. 이 경우 각각 정렬에 2 O(n log n) 비교에 O(2n)이 소요되므로 전체는 O( n log n)에 가능하다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
result: Set = set()
# 양쪽 모두 정렬
nums1.sort()
nums2.sort()
i = j = 0
# 투 포인터 우측으로 이동하며 일치 여부 판별
while i < len(nums1) and j < len(nums2):
if nums1[i] > nums2[j]:
j += 1
elif nums1[i] < nums2[j]:
i += 1
else:
result.add(nums1[i])
i += 1
j += 1
return result
Q. 정렬된 배열을 받아 덧셈하여 타겟을 만들 수 있는 배열의 두 숫자 인덱스를 리턴하라. (단, 배열은 0이 아닌 1부터 시작하는 것으로 한다.)
입력
numbers = [2,7,,11,15], target = 9출력
[1,2]
방법1. 투 포인터
이 문제는 정렬되어 있기에 투 포인터로 풀 수 있다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left, right = 0, len(numbers) - 1
while not left == right:
if numbers[left] + numbers[right] < target:
left += 1
elif numbers[left] + numbers[right] > target:
right -= 1
else:
return left + 1, right + 1 # 리턴 값 +1
방법2. 이진 검색
- 현재 값을 기준으로 나머지 값이 맞는지 확인하는 형태의 이진 검색 풀이를 시도할 수 있다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
left, right = k + 1, len(numbers) - 1
expected = target - v
# 이진 검색으로 나머지 값 판별
while left <= right:
mid = left + (right - left) // 2
if numbers[mid] < expected:
left = mid + 1
elif numbers[mid] > expected:
right = mid - 1
else:
return k + 1, mid + 1
방법3. bisect 모듈 + 슬라이싱 제거
- 바이섹트 모듈을 활용하면서 슬라이싱으로 최적화한 풀이이다.
import bisect
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
expected = target - v
i = bisect.bisect_left(numbers, expected, k + 1)
if i < len(numbers) and numbers[i] == expected:
return k + 1, i + 1
파이썬 슬라이싱 성능에 대해서
파이썬의 슬라이싱은 매우 효율적이고 빠르다고 했는데 배열의 길이를 계산할때 왜 오버헤드가 발생할까?
그 이유는 슬라이싱은 매번 새롭게 객체를 생성해서 할당하게 되고, 엄청나게 큰 배열의 경우 슬라이싱으로 새로운 객체를 생성하는 데 상당한 시간이 들기 때문이다. 마찬가지로 배열의 길이를 계산하는 데도 매번 길이를 계산하는 비용이 들기 때문에, 여기에 상당한 오버헤드가 소요된다. 슬라이싱을 하지 않을 경우 배열의 길이는 별도 속성으로 미리 계산하여 갖고 있으므로 해당 속성을 리턴하기만 하면 되지만, 슬라이싱은 매번 새롭게 배열의 길이를 계산해야 한다.
a = [1,2,3]
id(a) // 437...
b = a
id(b) // 437...
c = a[:]
id(c) // 438...
만약 매우 큰 배열의 경우 슬라이싱을 하게 되면, 전체를 복사하는 과정이나 배열의 길이를 계산하는 부분에서 상당한 시간이 소요되므로 주의가 필요하다.
비트 조작에 대해서 알아보자
원래 비트를 조작하는 것은 하드웨어와 관련이 깊다. 현대에 이르러 비트 조작 기법은 하드웨어뿐만 아니라 다양한 부분에 널리 활용된다. 여기서는 수학적 표기보다는 컴퓨터 과학에서 쓰이는 표기와 코드를 기준으로 살펴본다.
True and FalseTrue or Falsenot TrueTrue ^ TrueFalse (XOR)
~ True-2 (비트 연산자의 NOT은 2의 보수에서 1을 뺀 값과 같기 때문) , x = -x -1
bin(0b0011 * 0b0101)'0b1111'
bin(0b1101 >> 2)'0b11'
bin(0b1101 <<2)'0b110100'
bin(0b0101 ^ ~0b1100)'-0b1010'
0b1100은 십진수로 12다. 비트 연산자 NOT 결과는 십진수로 -12-1 = -13이 된다. 이를 2의 보수로 표현하면
111111...1110011이다. 이를 XOR 한 결과는 1111111...110110이 되며, 2의 보수로 표현하면 이 값은 -10이 된다.
파이썬의 진법 표현
bin(87) // 0b1010111 (string)
int('0b1010111',2) // 87
int ('1010111',2) // 87 (0b 생략가능)
format(87,'b') // 1010111
2의 보수에 대해서
2의 보수는 컴퓨터가 음수를 저장하기 위해 일반적으로 취하는 여러 방법 중 하나다. 여기서는 계산의 편의를 위해, 4비트 레지스터를 가정하고 표현하겠다. 양수만 저장한다면 0~15까지 저장할 수 있지만 음수도 저장해야 되기 때문에 절반을 쪼개서 음수 몫으로 할당한다. 맨 앞 비트는 부호 비트로 사용한다. 즉 0111은 7이지만 1000은 -8, 1111은 -1이 된다.
다만 파이썬은 2의 보수를 표현하지 않고 bin(-5) = '-0b101'처럼 정수에 -를 붙여 표시해준다.
그렇다면 양수를 음수로, 음수를 양수로 바꾸는 작업인 2의 보수 수학 연산은 어떻게 할까?
이는 비트 연산자 NOT을 한 후에 1을 더하면 된다.
정리하면,
1. 비트 연산자 NOT = 2의 보수에서 1을 뺀 것
2. 2의 보수 수학 연산 = 비트 연산자 NOT에서 1을 더한 것
0111의 2의 보수
1000 + 1
1001의 비트 연산자 NOT
0111 -1 = 0110
Q 두 정수를 입력받아 몇 비트가 다른지 계산하라.
입력
x = 1, y = 4출력
2
자연어 처리에서도 널리 쓰이는 해밍 거리는 두 정수 또는 두 문자열의 차이를 말한다. 이진수의 경우 다른 위치의 비트 개수가 된다. 이는 XOR 연산을 하면 쉽게 풀 수 있다.
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
return bin(x ^ y).count('1')
Q. 딱 하나를 제외하고 모든 엘리멘트는 2개씩 있다. 1개인 엘리멘트를 찾아라!
입력
[4,1,2,1,2]출력
4
XOR은 입력값이 서로 다르면 true, 동일하면 False가 되는 논리 게이트이다. 두 번 등장한 엘리먼트는 0으로 초기화되고, 한 번만 등장하는 엘리멘트는 그 값을 온전히 보존한다.
class Solution:
def singleNumber(self, nums: List[int]) -> int:
result = 0
for num in nums:
result ^= num
return result
출처 : 파이썬 알고리즘 인터뷰, 박상길 지음, 장진호 일러스트
'[코딩테스트 대비]' 카테고리의 다른 글
| TIL - 파이썬 (0) | 2021.10.23 |
|---|---|
| 알고리즘 - 슬라이딩 윈도우 (0) | 2021.10.07 |
| 코딩 테스트 대비를 위해 알아두면 좋은 팁 (0) | 2021.10.03 |
| 알고리즘 - Brute Force & DFS/BFS (0) | 2021.09.21 |
| 알고리즘 - [프로그래머스] 방의 개수 (Python) (0) | 2021.09.21 |